 Greeks, Time And Commensurability
Commensurability is often described in terms of length. Two lengths
are commensurable if there is a ratio between the two of whole measure.
If one length is two units and the other say 45/37 the length of the
first, then there is a correspondence of 74 of the first to 45 of the
second that are equal measures of the unit.
Simple as it sounds from our understanding of fractions this was a
big deal to the Greeks. Why this was so important is that the
relationships are independent of the units used. The relationship is the
same for units of inches, metres or miles. Nevertheless the thing
measured must be the same, or else just numbers. One couldn't compare
volume to speed etc.
Likewise there are numerous irrational numbers that are not
commensurable: Pi, the ratio of a circle's diameter to it's
circumference is an example. It was a point of debate that there was no
unit of choice that would make such numbers commensurable. Also, there
were relationships (such as like the distance covered by a body at a certain
speed), that are not entirely independent, but are proportional and when
examined with the idea of commensurability many paradoxes arise
that show that these measures (speed, distance) if commensurate, would allow the paradox that motion
would be impossible. Commensurability of these using the unit of time
(as with inches) to relate speed and distance is arguable from the view
that the 'present' is the constant, and not the 'length' of time
passing.
Here follows a few of those paradoxes. (Taken from Carl B. Boyer's
book "A History of Mathematics")
..."Aristotle described a Pythagorean point as "unity having
position" or as "unity considered in space." It has been suggested that
it was against such a view that Zeno propounded his paradoxes, of which
those on motion were cited most frequently. As they have come down to
us, through Aristotle and others, four of them seemed to have caused the
most trouble: (1) the Dichotomy, (2) the Achilles, (3) the Arrow, and
(4) the Stade. The first argues that before a moving object can travel a
given distance, it must first travel half this distance; but before it
can cover this, it must travel the first quarter of the distance; and
before this, the first eighth, and so on through an infinite number of
subdivisions. The runner wishing to get started, must make an infinite
number of contacts in a finite time; but it is impossible to exhaust an
infinite collection, hence the beginning of motion is impossible.
The
second of the paradoxes is similar to the first except that the infinite
subdivision is progressive rather than regressive. Here Achilles is
racing against a tortoise that has been given a head start, and it is
argued that Achilles, no matter how swiftly he may run, can never
overtake the tortoise, no matter how slow it may be. By the time that
Achilles will have reached the initial position of the tortoise, the
latter will have advanced some short distance; and by the time Achilles
will have covered this distance, the tortoise will have advanced
somewhat further; and so on the process continues indefinitely, with the
result that the swift Achilles can never overtake the slow tortoise.
The Dichotomy and the Achilles argue that motion is
impossible under the assumption of the infinite sub divisibility of
space and time; the Arrow and the Stade on the other hand, argue that
motion is equally impossible if one makes the opposite assumption - that
the sub divisibility of space and time terminates in indivisibles. In the
Arrow, Zeno argues that an object in flight always occupies a space
equal to itself; but that which always occupies a space equal to itself
is not in motion. Hence the flying arrow is at rest at all times, so
that it's motion is an illusion.
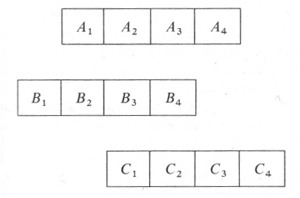
Most controversial of the paradoxes on motion, and most
awkward to describe, is the Stade (Or Stadium), but the argument can be
phrased somewhat as follows. Let A1, A2, A3, A4 be bodies of equal size
that are stationary; let B1, B2, B3, B4 be bodies, of the same size as
the A's, that are moving to the right so that each B passes an A in an
instant - the smallest possible length of time. Let C1, C2, C3, C4 also
be of equal size with the A's and B's and let them move uniformly to the
left with respect to the A's so that each C passes each A in an instant
of time. Let us assume that at a given time the bodies Occupy the
following positions:
Then after the lapse of a single instant - that is,
after an indivisible subdivision of time - the positions will be as
follows:
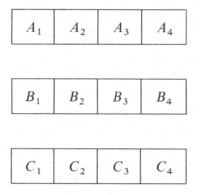
It is clear, then that C1 will have passed two of the
B's; hence the instant cannot be the minimum time interval, for we can
take as a new an smaller unit the time C1 takes to pass one of the B's.
The Arguments of Zeno seem to have had a
profound influence on the development of Greek Mathematics, comparable
to the discovery of the incommensurable, with which it may have been
related. Originally, in Pythagorean circles, magnitudes were represented
by pebbles or calculi from which our word calculation comes, but by the
time of Euclid there is a complete change in point of view." - (taken
from "A History of Mathematics" Chapter V section 11, by Carl B. Boyer,
Wiley International Edition)
Sometimes however, efforts similar to this early Greek use of time as
a unit of commensurability has real world application. Astronomy near
grounded to a halt with observed disparity between the magnitude of
spectra of starlight and the modelled predictions. It was discovered
that a substitution of E=hf, (E energy, f frequency, and h a constant)
within the model provided an inter-relation of E and f that accurately
predicted the detected spectra when taken into account.
So what use is this to understanding dialectic logic? Simply the assumption that everything logical is also commensurable. The inversion of thesis/antithesis to the inconsistency between the two remaining balances of the four (as in synthesis) leads to the method using those two outcomes (incompatible with each other) as commensurable - the thesis/antithesis from which the two negations arise must be "married" as commensurate if the method is to be held correct.
The method then takes two opposing factors that may never agree and itself as the conjunction, supplies a "common measure" where the method is itself synthesis, commensurating the opposition of thesis/antithesis.
Likewise any two opposites birth two new opposites that birth the starting pair: we have the stance of "as above, so below" that is intrinsically deceptive and a tenet of satanism, direct from the serpent. Being able to quickly adapt the principle and give the appearence of commensurability with the method is the very heart of the work of satan, deception.
Continue To Next Page
Return To Section Start
Return To Previous Page |